Digital Learning Environments (DLEs) for math are created with the aim of building students’ mathematical thinking, knowledge, and skills. It is therefore critical that such DLEs are grounded in relevant theoretical frameworks. Such frameworks are needed to assess students’ prior knowledge, address misconceptions, promote mathematical ways of thinking, and adopt an evidence-based approach to the design of DLEs for math.

DLEs for Mathematics

In my previous article on Theory-Driven Digital Learning Environments (DLEs) for Mathematics,^[1] I highlighted key features to consider when identifying an appropriate theoretical framework for DLEs for math. Specifically for topics from secondary and high school curricula, a framework that addresses their complex and hierarchical nature and accounts for “how” learners build their mathematical understanding is important. One such framework is the Action, Process, Object, and Schema (APOS) framework^[2]. This article describes the APOS framework and how it can be applied to assess student learning in DLEs.

If you’re a teacher, assessment designer, or instructional designer of mathematical learning experiences, this article will provide you with an overview of APOS. It will serve as an introductory guide to understanding and applying APOS to mathematical concepts. More generally, it uses the example of APOS to provide a structure for analyzing students’ problem solving and how they can be applied to inform the design of DLEs.

Why APOS?

APOS can be a robust theoretical framework for DLEs for math due to a variety of reasons. APOS is specific to mathematics and hence considers the complex, hierarchical, and interrelated nature of concepts. Yet, it is sub-domain agnostic and can be applied to the full range of mathematical concepts from geometry, algebra, calculus, etc. Additionally, it accounts for the variety of strategies that students might adopt in solving mathematical problems. This is crucial to encourage open ended thinking in mathematics and go beyond the “one-correct solution/approach” mindset. Finally, APOS has been widely used to assess students’ mathematical problem solving on a range of different topics^[3]. Moreover, it has also been used to inform curriculum design and instruction of higher level mathematics topics^[4].

What is APOS?

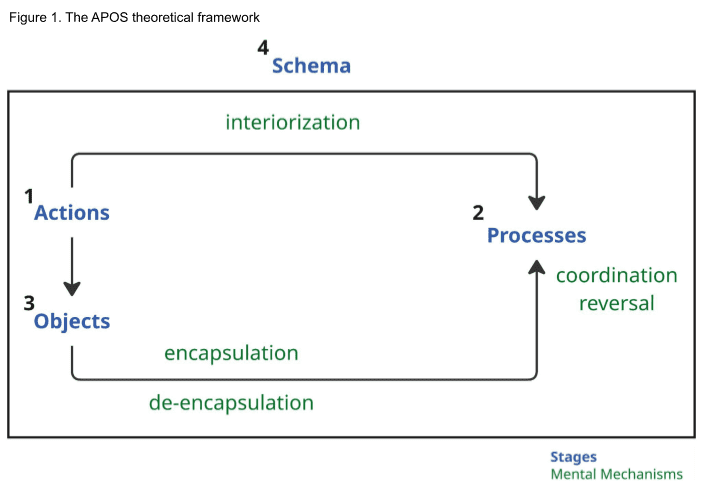
APOS argues that students engage in mathematical problem solving via construction and application of mental structures associated with mathematical concepts. The “stage-based” structure of APOS covers the central aspect of advanced mathematical concepts: their hierarchical nature. According to APOS, students build an understanding of higher order concepts by transforming their knowledge of previously established mental structures. The four stages of APOS are Action, Process, Object, and Schema.

1. At the first stage, students simply perform explicit “Actions” to apply a concept and solve problems. At this stage they do not have a deeper conceptual understanding but enough procedural knowledge to solve problems by taking a step-by-step, algorithmic approach.
2. As students repeatedly perform these Actions, they are “interiorized” to build a deeper understanding and transformed into “Processes”. At this “Process” stage, students are able to skip steps entirely or do not feel the need to perform them explicitly. They are able to carry out the Actions (e.g., procedural steps, calculations) in their mind. “Interiorization” is the mental mechanism that is needed to go from the Action stage to the Process stage. At this stage, students can also reverse Processes and break them down into Actions.
3. When Processes are solidified with further deeper understanding, they become “Objects” via “encapsulation”. At this stage, students can apply operations and Actions on the entire Process itself. “Encapsulation” is the mental mechanism needed to go from the Process stage to the Object stage. Students at the Object stage can also “de-encapsulate” the Objects to Processes, “reverse” Processes into Actions and “coordinate” multiple Processes to solve mathematical problems.
4. Finally, the Schema stage refers to the interplay and collection of all Actions, Processes, and Objects associated with a concept. Students at the Schema stage of a concept can apply that concept in different scenarios and also combine it with other concepts to solve complex mathematical problems. Further, due to the hierarchical nature of mathematical concepts, having a Schema level understanding of foundational concepts is necessary to build an understanding of higher order concepts. For example, a Schema level understanding of multiplication is necessary for students to develop any level of understanding of the concept of Percentages.

Let us consider the example of the mathematical concept of calculating the “mean” of a dataset from the lens of APOS^[5]. Students at the Action stage can correctly apply the steps for calculating the mean of a given data set by adding all the values and dividing the sum by the cardinality of the set. However, they do not yet understand what kind of central tendency is represented by the mean. It is only after they have “interiorized” the steps involved in calculating the mean of a data set and are at the Process stage of APOS, that they can describe in general how the mean can be calculated for any data set and what it represents. They can describe the reasoning behind the order of steps involved in calculating the mean (e.g., why elements are added and not multiplied, why the sum is divided by the cardinality). Then, at the Object stage, students have encapsulated the processes of calculating the mean. They can grasp the mean as one of the measures of central tendency. They can make inferences, comparisons, and draw conclusions about the nature of data sets based on their means. Finally, at a deeper Schema stage, students can interrelate all the Actions, Processes, and Objects associated with the mean. They can mentally draw conclusions about the changes in the mean of a data set when one or more values are changed without recalculating it from scratch. They are able to interpret the effect of extreme values on the mean. They are also able to comprehend how mean and other measures of central tendency (e.g., median) are conceptually different from each other.

Applying APOS to Support and Assess Learning in DLEs

APOS is based on the premise that students can “learn any mathematical concept provided the structures necessary to understand those concepts have been built”^[6]. A DLE can provide interactive tools that support students’ construction of such mental structures. According to APOS, students deal with mathematical problems by constructing and applying mental structures2. Due to the hierarchical nature of mathematics, making lower level structures is fundamental for students to construct more robust and complex higher-level constructions4. Identifying and defining what students can do at each stage is the first step of APOS-based modelling of student learning. This is called creating a Genetic Decomposition (GD) of a mathematical concept. When applying APOS to guide the development of DLEs, students’ interactions within the DLE, use of tools and their order, voice commands, and inputs can be mapped to each element of the GD. Hence, as students solve problems and interact with the DLE, a rich stream of data is analyzed and mapped to the APOS-based GD. This can be used to identify the knowledge level of students and hence offer appropriate interventions to further build their understanding.

It is also important to consider some limitations of APOS in the context of DLE research and development cycle. The GD created by the research team is the first piece of applying APOS. However, it is possible that students pursue different learning paths than those outlined in the GD^[7]. Hence, the role of empirical verification becomes critical. A GD can serve as an appropriate model of mathematical cognition of learners only when its efficacy is tested with empirical evidence that describes students’ conceptions and problem solving strategies. As researchers around the world use APOS-driven research cycles and create GDs for a range of topics⁶, it is observed that the theoretical modelling via GDs increases the reliability of the analysis of students’ responses and also serves as a diagnostic and predictive tool⁶. Finally, it is also worth noting that one GD of a concept created by researchers is not unique. Instead, it is a theoretical model that can help understand the thinking of most students⁶.

Additionally, it is not possible for one theoretical framework to consider all aspects of mathematical learning. While APOS is math-specific, one critical aspect of mathematical learning that it does not address is “misconceptions”. Conceptual and procedural misconceptions are a common problem in mathematical knowledge of students^[8]. Misconceptions associated with foundational concepts can have compounding adverse effects on students’ understanding of higher level concepts^[9]. The stages and mental mechanisms of APOS do not account for the range of misconceptions students’ that might be associated with the concept. It is possible that a student is at a higher level of understanding (e.g., Object) but still possesses some misconceptions associated with a lower level (e.g, Process) or topic. For instance, misconceptions associated with fractions can be detrimental to students’ conceptual understanding of percentages^[10]. Hence, it is also crucial to include misconceptions as part of the GDs constructed for APOS when it is applied to design DLEs. In addition to defining the elements of Action, Process, and Object stages of a concept, elements associated with Misconceptions can also be added to the GD. This takes a step-forward in the theoretical development of APOS and also extends its applicability to understanding and linking students’ actions with possible misconceptions. When students’ interactions within the DLE are mapped to the APOS-based elements of the GD, those that represent common misconceptions can also be mapped to their corresponding elements. This can yield crucial insights into students’ understanding of mathematical concepts. Moreover, it also provides a broader and holistic assessment of students’ understanding that goes beyond identifying if they answer correctly or not. It identifies their level of understanding from the lens of mathematical cognition and highlights some misconceptions that they might possess which can be rectified with remedial instruction.

The Way Forward

APOS can be a relevant and useful theoretical framework for grounding DLEs for math in evidence-based research. APOS-based instruction and assessment is grounded in the hypothetical genetic decomposition (GD) of concepts created by education researchers. However, without empirical evidence, a GD remains merely a hypothesis that needs to be tested using empirical data.

Applying APOS to design interactive DLEs for math requires mapping of students’ actions, use of tools, and description of knowledge to APOS stages. Different types of students’ interactions, order of tool use, and responses can be analysed based on APOS and used as evidence of understanding. The findings are then used to improve the GD and identify strategies for remedial instruction and intervention. Such research-based assessment cycles can provide deeper insights into students’ knowledge and mathematical thinking.

Theory and evidence-based assessment using DLEs can utilize their potential to capture moment-by-moment data as students solve mathematical problems. It can pave the way for taking advantage of DLEs to go beyond “one-size fits all” and “one correct answer” approaches to assessment of mathematical knowledge. It also has the potential to build and provide adaptive opportunities to support students’ learning and deeper assessment of their mathematical knowledge.

---

About the Author

Robin Sharma is a creator of science-based, digital learning environments (DLEs). He has over seven years of international experience in conceptualizing, implementing, and evaluating educational programs. As Vretta’s Learning Scientist, he is working with the Innovation Team to create an AI-driven problem solving canvas for high school mathematics grounded in the science of mathematical thinking. Robin has expertise in mathematics education, digital-game based learning, and curriculum development. He also works at the Technology, Learning, and Cognition Lab at McGill University where he studies factors influencing teachers’ adoption of digital games into classrooms and theory-based design of math games.
Previously, he managed the “Games for Learning” program at UNESCO MGIEP. He developed curriculum guides, educator toolkits, and several MOOCs on educational games. He led and co-authored the UNESCO guidelines on digital learning, a set of principles for ethical and responsible development of DLEs aligned with UNESCO’s framework on Education for Sustainable Development (ESD) and social-emotional learning (SEL). Robin has also worked in the videogame industry, developing the world’s first, interactive, gaming curriculum guides for teachers. These guides aim to support educators’ adoption of the immersive Assassin’s Creed Discovery Tour video games by Ubisoft. He has won several awards, scholarships, and grants including the International Doctoral Research Award from IDRC Canada and the FRQSC Doctoral Fellowship from the Government of Quebec. Robin is an active member of the EdTech Impact Network managed by the International Center for EdTech Impact , Mathematics Teachers Association, and Game Research and Design Community (GRADE).

---

References

[1] Theory-Driven Digital Learning Environments (DLEs) for Mathematics: https://www.vretta.com/buzz/theory-driven-digital-learning/

[2] Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Fuentes, S. R., Trigueros, M., & Weller, K. (2014). From Piaget’s Theory to APOS Theory: Reflective Abstraction in Learning Mathematics and the Historical Development of APOS Theory. In I. Arnon, J. Cottrill, E. Dubinsky, A. Oktaç, S. Roa Fuentes, M. Trigueros, & K. Weller (Eds.), APOS Theory: A Framework for Research and Curriculum Development in Mathematics Education (pp. 5–15). Springer. https://doi.org/10.1007/978-1-4614-7966-6_2

[3] Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Fuentes, S. R., Trigueros, M., & Weller, K. (2014). The APOS Paradigm for Research and Curriculum Development. In I. Arnon, J. Cottrill, E. Dubinsky, A. Oktaç, S. Roa Fuentes, M. Trigueros, & K. Weller (Eds.), APOS Theory: A Framework for Research and Curriculum Development in Mathematics Education (pp. 93–108). Springer. https://doi.org/10.1007/978-1-4614-7966-6_6

[4] Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Fuentes, S. R., Trigueros, M., & Weller, K. (2014). The Teaching of Mathematics Using APOS Theory. In I. Arnon, J. Cottrill, E. Dubinsky, A. Oktaç, S. Roa Fuentes, M. Trigueros, & K. Weller (Eds.), APOS Theory: A Framework for Research and Curriculum Development in Mathematics Education (pp. 57–91). Springer. https://doi.org/10.1007/978-1-4614-7966-6_5

[5] Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Fuentes, S. R., Trigueros, M., & Weller, K. (2014). Mental Structures and Mechanisms: APOS Theory and the Construction of Mathematical Knowledge. In I. Arnon, J. Cottrill, E. Dubinsky, A. Oktaç, S. Roa Fuentes, M. Trigueros, & K. Weller (Eds.), APOS Theory: A Framework for Research and Curriculum Development in Mathematics Education (pp. 17–26). Springer. https://doi.org/10.1007/978-1-4614-7966-6_3

[6] Dubinsky, E. (1991). Reflective Abstraction in Advanced Mathematical Thinking. In D. Tall (Ed.), Advanced Mathematical Thinking (pp. 95–126). Springer Netherlands. https://doi.org/10.1007/0-306-47203-1_7

[7] Arnon, I., Cottrill, J., Dubinsky, E., Oktaç, A., Fuentes, S. R., Trigueros, M., & Weller, K. (2014). Genetic Decomposition. In I. Arnon, J. Cottrill, E. Dubinsky, A. Oktaç, S. Roa Fuentes, M. Trigueros, & K. Weller (Eds.), APOS Theory: A Framework for Research and Curriculum Development in Mathematics Education (pp. 27–55). Springer. https://doi.org/10.1007/978-1-4614-7966-6_4

[8] Shimizu, Y., & Kang, H. (2025). Research on classroom practice and students’ errors in mathematics education: A scoping review of recent developments for 2018-2023. ZDM – Mathematics Education, 57(4), 695–710. https://doi.org/10.1007/s11858-025-01704-0

[9] Stemele, B. P., & Asvat, Z. J. (2024). Exploring Learner Errors and Misconceptions in Algebraic Expressions with Grade 9 Learners Through the use of Algebra Tiles. African Journal of Research in Mathematics, Science and Technology Education. https://www.tandfonline.com/doi/abs/10.1080/18117295.2024.2334989

[10] González-Forte, J. M., Fernández, C., Van Hoof, J., & Van Dooren, W. (2023). Incorrect Ways of Thinking About the Size of Fractions. International Journal of Science and Mathematics Education, 21(7), 2005–2025. https://doi.org/10.1007/s10763-022-10338-7