For decades, assessments across the field of education, both paper and digital, have used test scores as the principal measure of student learning. A student gets a question right or wrong, and that's the end of the story. But what if we could see how they arrived at their answer in the digital setting? A recent research article¹ by de Schipper et al. explores this very question, demonstrating how the digital breadcrumbs students leave behind (their process data) can reveal their problem-solving strategies and offer a much deeper understanding of their learning.

Case Study: Modelling a Calculation Program

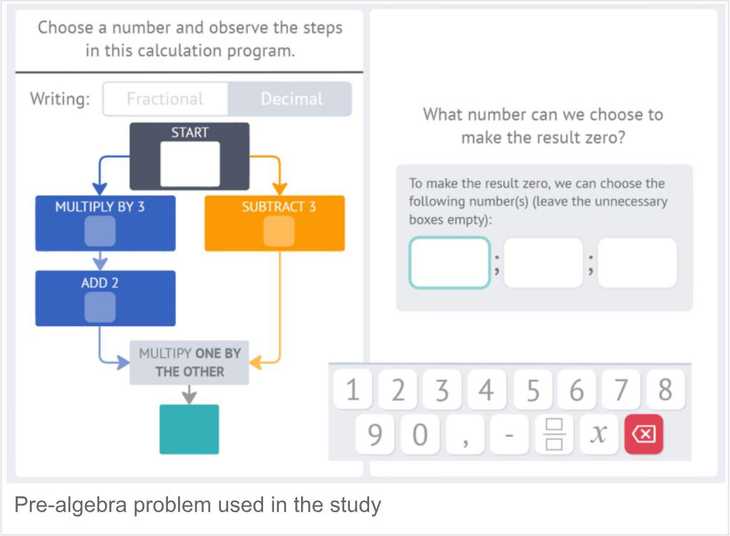
The study, as described in the research article, analyzed how 802 ninth-grade students in France tackled a single interactive, pre-algebra problem. The item required students to find the input values that would make the result of a calculation zero. The digital interface included an embedded calculation where students could test values.

A seasoned math enthusiast will notice that the core of the problem can be represented by the equation (3x+2)(x-3)=0

with the correct answers being x=3 and x= ⅔

Students could theoretically solve this problem in two ways:

1. Algebraic (Structural) Approach: Recognizing the structure of the equation and knowing that a product is zero only if one of its factors is zero. This requires abstract thinking.
2. Trial and Error (Operational) Approach: Systematically or randomly plugging numbers into the calculator to see what works. This is a process-based strategy.

By analyzing the process data produced by the students’ actions, the researchers used model-based cluster analysis to group students based on their behaviour.

Key Findings

The analysis didn't just find two groups; it identified five distinct behavioral profiles. These groups varied significantly in their approach:

• Some students quickly found the easy answer (x=3) and stopped.
• Others engaged in extensive trial and error, sometimes finding both correct answers.
• A notable group showed behaviour consistent with an algebraic approach, spending less time interacting with the calculator and more time thinking.
• One group was characterized by very little interaction and extremely low success rates. This group was found to have a significantly lower overall mathematics ability compared to the other four groups.

These findings show that the process a student follows is not only a powerful indicator of their mathematical ability, but also provides a more nuanced portrait of their overall understanding.

The Path Forward: Problem-Solving Canvases

This study is a powerful proof of concept that inspires further avenues of investigation. One such avenue is to create a digital assessment environment that allows students to explore solution strategies while facilitating the collection of their process data. An example of such an environment is a problem-solving canvas.

A problem-solving canvas is not just a test item; it's an integrated digital workspace designed to both present a complex problem and capture a rich spectrum of strategic actions. Imagine a student tasked with a physics problem. The canvas wouldn’t just be a question and an answer box. It would include:

• A space for students to capture their ideas, notes, and equations.
• An interactive simulation or diagram, if appropriate for the problem..
• Graphing tools and calculation tools.
• Access to a glossary or formula sheet.

Every interaction a student has with the workspace, be it drawing a free-body diagram, changing a variable in the simulation, using the calculator, or looking up a formula, helps to build a picture of their cognitive and behavioural processes.

Unlocking Deep Learning Patterns with AI

By feeding this rich, multi-modal process data into safe and secure AI models, it is possible to unlock further learning patterns that will help educators understand the entire problem-solving narrative. The following are a few ways in which such learning patterns can be unlocked:

• Assembling Framework: By gathering the steps taken by a student on the path to a solution, we can build a framework of their knowledge, offering a detailed model of their understanding of the problem and how this understanding fits inside the subject area as a whole.
• Personalized, Just-in-Time Feedback: An AI-powered canvas could detect when a student is engaged in unproductive behavior, such as randomly guessing. It could then offer a scaffolded hint, not giving the answer, but suggesting a more systematic approach (for example, "Have you tried organizing your trials in a table?").
• Informing Teachers: At the class level, this data is transformative. A teacher's dashboard could show that 40% of the class isn't using the graphing tool to visualize functions, revealing a gap in instruction. It allows teachers to move from remediating wrong answers to proactively teaching effective problem-solving strategies.

By combining process data from digital workspaces with intelligent analysis, we can transform assessment to provide rich, personalized learning experiences for each student. It evolves from being a final judgment to a dynamic, insightful, and supportive part of the journey itself, giving us a window into the most important part of education: how students think.

---

About the Author

Mitch Haslehurst is a research mathematician with expertise in algebra and geometry. He earned his Ph.D. in mathematics from the University of Victoria, and his work has been published in leading journals, including articles in the Journal of Operator Theory and the Rocky Mountain Journal of Mathematics. He has presented at conferences across North America and Europe.

Currently, Mitch works with Vretta, where he applies his mathematical expertise to the development of innovative assessment and learning solutions, and the advancement of research projects. His role bridges research with educational practice, reflecting his commitment to making complex ideas both accessible and impactful.

He is driven by curiosity, creativity, and a dedication to advancing mathematics while applying knowledge to real-world challenges. You can connect with him on LinkedIn.

---

References